How luck arises in skill-based competitions
Louigi Verona
December 2020
I. Problem statement and goals
In many modern societies the underlying assumption behind attitudes towards success is meritocracy. On the basis of that assumption people are rewarded for past accomplishments, which are treated as evidence of skill/competency.
Scientific literature, however, seems to point to a role of luck more prominent than is typically assumed. The very known paper by Pluchino, Biondo and Rapisarda titled "Talent vs Luck: the role of randomness in success and failure" shows that most successful individuals tend to have slightly above average talent and lots of luck, and that the reason for this disparity is the positive feedback loop that is embedded in the meritocracy assumption: if someone is provided a lucky opportunity and they are skilled enough to put it to use, they are likely to get an advantage in the future. The beauty of their model is its simplicity, very reasonable assumptions that go into it, and clear results.
In this paper I suggest a different take on the problem: instead of modeling specific situations, I propose a framework to describe any competition. The framework is indiscriminate towards scale. It is capable of modeling any competition, whether it is a short game between two people or a competition between all people in the world for success in life as a whole.
The surprising outcome of this general approach is that it shows exactly where the unfairness comes from, and that it arises even when the competition setup is as fair as possible.
Additionally, the framework illuminates situations in which skill would actually matter more than luck. The reason why I find this important is that it allows us to explain the perception that many of us have of the importance of skill in life without appealing to cognitive bias alone: in some situations skill is, in fact, more important than luck.
And so, the goals of this paper are the following:
- Suggest a framework that can be used as a tool to analyze the role of success and luck in any competition, akin to how the Bayes theorem can be used to assess probability
- Demonstrate how luck-dominated situations occur regardless of the ratio of skill to luck, thus explaining the counter-intuitive nature of the high role of luck in success
- Outline the conditions when skill does actually matter more than luck, explaining exactly why skill is still a factor in success, albeit to a much lesser degree than luck - and why this degree is lesser
- Demonstrate that most unfairness stems not from the amount of luck inherent in the activities themselves, but by rules of how ranks are assigned to players
The framework describes a competition with players.
The performance of players in a competition is quantified by a score.
A score is defined as a sum of skill and luck.
A score ranges between 0 and 1.
The behavior of luck is modeled as a random number generator, potentially ranging from -0.5 to 0.5. So, luck_limit is the amplitude of randomness. It can be set to lower values, if one wishes to model a system with less luck.
Skill can range from 0 to 1-luck_limit.
score = skill + random(-luck_limit, luck_limit)
A visual representation of how the score calculation works is this:
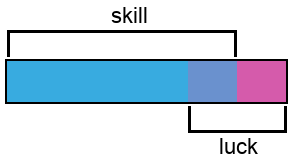
The ratio of skill to luck is defined by the nature of the competitive activity the players are engaged in and by the competition rules. Essentially, the nature of the activity defines the ratio, and competition rules act as a modifier of that ratio: certain rules might decrease the role of skill and increase the role of luck, for example.
Additionally, the model introduces a rank ladder - a list of players ordered by their rank. A ladder state is an instance of a ladder:
| Rank 1 | Player 5, Player 2 |
| Rank 2 | Player 30 |
| Rank 3 | Player 14, Player 1 |
| ... | |
| Rank N | Player n, Player m |
A ladder has ranking rules, which define how the score influences player rank.
A fair ladder will take into account only the score. Real-life ladders usually take into account more than just a player's score.
The difference between competition rules and ranking rules
It is imperative that the difference between competition rules and ranking rules is understood. Policies of translating player performance into rank may very strongly affect a ladder state.
To clarify these terms further, we can use an example of a tennis tournament.
Here, competition rules are going to be the rules of the game of tennis itself.
Ranking rules is everything that is applied on top of that, specifically: how the competition is run (having a knockout tournament, for example), seeding the players, tennis associations assigning skill level to players that then inform how they get matched up in tournaments, the use of tiebreakers if players have the same amount of points, etc. Obviously, these ranking rules are capable of dramatically changing the positions of players on rank ladders, while having the rules of the game of tennis stay the same.
In other words, differentiating between competition rules and ranking rules provides an additional and very relevant dimension to the model. This could even be argued to be the most important dimension of the model, since, frequently, unfairness stems not from the competition rules, but from the way the players are ranked.
In order to make this clearer, I even considered using the term "competition activity", since in many cases we would use the term "competition" to denote competition rules and ranking rules together. But the term "competition activity rules" is awkward, so for the purposes of brevity, when I use the term competition rules in this paper, I only mean the rules of the competition activity itself, and not also the ranking rules.
"Competition" is descriptive
When I am using the term "competition", I am using it in a descriptive sense: it can be applied to any situation where performance can be ranked.
For instance, if we take the population of a country, we can rank people based on their command of the country's official language. There is no "language competition", but we can model the situation as such.
Therefore, saying that something is a competition is not to say that people are actually visibly and consciously competing.
Variable luck_limit
In competitions analyzed in this paper, luck_limit will stay at a fixed value. It also makes sense for it to stay fixed for many real-life situations, too. For instance, in tennis the amount of luck in the game will stay the same throughout. However, there are competitions where luck_limit will actually change.
A good example is a poker tournament. Raising the blinds can be described as increasing luck_limit. A multisport race like triathlon would change luck_limit three times, since swimming, cycling and running could be argued to have different luck_limits.
Changing luck_limit, however, might be a way to model more complex interactions. For instance, one might decide to create a relationship between the amount of skill and the amount of luck: the lower the skill, the more luck is involved.
Luck can also be modeled to be asymmetrical: instead of having it work as random(-luck_limit, luck_limit), two separate variables could be used, so that luck could be made to only help or only hurt performance: random(-lower_luck_limit, upper_luck_limit).
Let's take a simple case of a competition with many players that has a rank ladder.
The ladder is fair, in a sense that
- the place on the ladder is defined solely by the score - the higher the score, the higher one is on the ladder
- the rule is applied to all players without discrimination
The competition is run many times and the goal is to assess the variability of ladder states over time.
Case 1. Absolute skill
In this scenario luck = 0. So, score = skill, where skill ranges from 0 to 1. Increasing skill increases one's position on the fair ladder.
The immediate implication of this is that it is likely that many players would end up with the same score and would occupy the same position on the ladder. If the values of skill stay the same, ladder states are going to be identical over time. The number of ranks is going to reflect the distribution of skill among the players.
It can be argued there is no activity in the real world that can be described as having no luck factor at all. There might be activities in which it is possible to attain a skill of 1, but the negative influence of luck will always be there, even if minuscule.
Case 2. Absolute luck
In this scenario skill is a 0 and luck_limit is always 0.5. Score = random(-luck_limit, luck_limit).
In this case, a fair ladder is going to be inconsistent over time. The overall number of ranks will tend to be higher than in the case of absolute skill.
Notice that for the score to be random, skill does not have to be set at 0, it just needs to be constant for all players. Of course, the higher the fixed skill in this scenario, the less variable the ladder is going to be, and it would also tend to have less ranks.
There are activities in the real world that can be described as having luck as the only variable. Playing slot machines, for instance, involves no skill.
Case 3. Non-zero luck_limit, fixed value
In this scenario luck_limit is set at some fixed value, which is below 1, and the rest is left for skill. Skill can grow from 0 up to 1-luck_limit.
This scenario is more complicated than the previous two, and it already helps demonstrate how luck plays a significant role in certain situations, regardless of the ratio of skill to luck.
Let's explore a case when the ratio is 95% skill and 5% luck_limit. This means that the score would be defined as
score = skill + random(-0.05, 0.05)
This would randomize the rank positions of players with similar scores over time, within the window of [score-luck_limit, score+luck_limit]. It would also slightly muddle the relationship between the distribution of skill and the number of ranks, with the tendency to increase the amount of ranks, since players with the same skill might end up on different ranks.
This slightly more complicated scenario already allows us to model two types of situations:
- when luck plays a dominant role
- when skill plays a dominant role
Imagine one player attaining a skill level of 0.95, the highest skill level possible. Even if they are immensely unlucky, their score would end up being 0.9, which is very high. However, imagine now that they are matched-up against a player whose skill level is also 0.95. Suddenly, the only thing that affects the outcome of their competition is luck.
In other words, when a competition is held between players of identical skill, the role of luck becomes absolute.
This is true regardless of the ratio of skill to luck, just as long the element of luck is non-zero, which is always the case in real-life situations. It stays true even in the case of the most fair ranking rules possible.
This becomes especially significant if the ladder is not fair, meaning that it has additional rules, like only one or several top ranks are considered winning, only a limited number of players can occupy a rank, and so on - exactly the kind of rules that frequently exist in real-life situations. So, even if a fair ladder would have situations with a very high or even absolute role of luck, less fair ladders are going to skew the ranking even more towards randomness.
But we can also qualify situations in which the role of skill is absolute.
If a competition is held between players of different skill levels, and if the difference between skill levels is larger than luck_limit x 2 (the full range of luck in a given competition), then the only thing that matters would be skill. In other words, no matter how lucky the less skilled player would be and no matter how unlucky the more skilled player would be, the more skilled player would still win.
I find these scenarios important, because it is an elegant way to describe the duality of our perceptions: as researchers, we notice that things are highly dependent on luck. And yet, it's difficult to ignore the very real element of skill. And while it is the element of luck that is absent from the public attitudes towards achievement and success, I feel that it's essential to come up with a model that is capable of demonstrating both types of cases, cases when luck is pivotal and cases when luck matters very little.
These scenarios also show why many researchers conclude that skill plays a lesser role: because the most meaningful competitions almost always involve people with similar skill levels, whereas competitions between players of very different skill levels are less dramatic and rarely paid much attention to.
This class of ladders does not allow ranks to be occupied by more than one player. If players end up having the same amount of points, a tiebreaker rule is used. This kind of ladder is used in most competitive sports, music charts, but can also describe everyday situations like job promotions.
The ordinal ladder becomes a problem if participants' skill levels are identical or very similar, as the need to assign a unique rank to every player might fail to reflect the actual ability of participants.
It is important to note that identical skill levels are not just a simplification used for demonstration purposes. It is a very real phenomenon, since the resolution of our methods of assessing skill levels is frequently low enough that we end up with ranking people on the same level. This might be less prevalent in sports, where ranking systems take into account many parameters, thus making ties unlikely.
But in many cases, even in cases when measuring performance is very important, participants are graded similarly. Education system is a good example here: many countries have a 5-10 points grading system. In the US, for instance, it is common to use the A-F grading system, with grades A, B and C being the most meaningful. This means that a lot of people whose skills are probably slightly different, are going to receive the same grade.
Another reason why skill levels could be identical is if the optimal skill level is easily attainable and verifiable, in which case people might actually have identical skills within the rules of the competition. For instance, if the point of the competition is to recite a number of finite length, it is possible that many or even all the competitors would recite it without error, and for the purposes of the competition this sort of resolution might be satisfactory.
But, of course, in many cases identical skill levels are incompatible with ranking rules. If the ladder is ordinal, then some sort of tiebreakers should be introduced.
One way to resolve this is to increase the complexity of skill: for instance, in tennis, a tiebreaker essentially adds more dimensions to a skill by counting participation in specific tournaments, including taking into account the highest amount of points in a single tournament.
Apart from giving more data points to compare and thus make it more likely to break a tie, increasing skill complexity leads to two additional side effects: first of all, it decreases the amount of potential players who would possess this kind of skill.
Second, It also tends to increase luck_limit, since having to accomplish more things means more things can go wrong, at least in the case of properly designed tiebreakers, since they want to take into account accomplishments which would be independent of the main score.
Additionally, applying skill complexity as a tiebreaker only to a select few, which is exactly how tiebreakers are applied, might be argued to actually introduce unfairness: if such a complex skill set was to be applied to all the players, the ladder state might become very different.
Now let's look at one of the most common tournament types that use an ordinal ladder - knockout tournaments.
Knockout tournaments
Knockout tournaments use an ordinal ladder. The tournament setup can be thought of as a clever tiebreaker, effectively preventing players from ever qualifying for the same rank.
The idea is that only several ranks would be considered winning, usually first, second and third. In order to get there, a series of rounds is organized, when players are matched up against each other, the losers are eliminated from the competition and the winners go on to the next round.
Sometimes the defeated competitors continue matches against each other to define further rank classification.
Match-up rules vary and can be completely random or defined by a set of parameters, like past performance.
A ladder state of a knockout ladder with three winning places would look something like this:
| Rank 1 | Player 5 |
| Rank 2 | Player 30 |
| Rank 3 | Player 14 |
Let's analyze two knockout ladder variations: without positive feedback and with positive feedback.
Case 1. Knockout tournament with no positive feedback
For simplicity's sake, let the competition be a 1:1 game, akin to chess tournaments. Players are randomly organized into pairs.
In the first round, 50% of the competitors are eliminated. 50% of the remaining players are eliminated in the next round, and so on, until 8 players are left to compete in the quarterfinals, then 4 players to compete in the semifinals and, finally, 2 players to compete in the finals, with a single winner emerging.
It is possible to rank all the eliminated players. If 128 players are competing, and half of them are eliminated in the first round, they should then compete for rank 64 in the same manner, then the players eliminated from that competition compete for rank 96, and so on, so that in the end we are left with an ordinal list of players by rank.
For this analysis, let us assume that the competition activity is mostly skill-based, with a very low luck_limit, and that all the players have identical skill.
It then becomes immediately clear that these ranking rules are inherently unfair: the input of the system receives over a hundred players with identical skill, yet one player would end up ranked at number 1 and another at number 128 - a dramatic difference!
The reason for this is that a knockout ladder forces ordinal ranking.
Of course, ordinal ranking would be a problem only for a single run. If we were to run the competition many times and then compare ladder states, we would be able to analyze their variance. In the case of identical skill levels, we would see a random distribution over time, with no player maintaining a steady position.
If players do actually have skill levels that could be ranked ordinally, then after the competition is run many times, we would see a pattern emerging across the ladder states that would allow us to derive actual skill levels. However, if players have very close or identical skill levels, then rank distribution within skill level clusters would end up being random each time.
So, the application of a knockout ladder is going to reflect actual players' skills only over long periods of time, but results of a single knockout tournament say very little, if anything at all, about players' actual skill levels.
Case 2. Knockout tournament with positive feedback
Now, let's take a look at a similar ladder, with a similar player setup: 128 players with identical skill levels. But this time we will introduce a positive feedback loop. Almost all knockout ladders in real life have either obvious or hidden positive feedback loops that favor previous winners.
Even without modifying the rules, the mere recognition that in real life we cannot run an infinite amount of competitions and that, in fact, nobody analyzes a series of competitions, but the players are instead rewarded here and now, already introduces a positive feedback loop: even if no money is involved, the motivation of someone who worked hard, but got place 128 is going to be markedly lower than that of someone who is declared champion.
Another hidden positive feedback mechanism is fame. Even if no monetary prizes are involved, the sheer fame and respect generated by winning a competition with ordinal rankings creates opportunities for the champion at the expense of the rest, including preferential treatment and potential income that allows one to continue to engage in the activity professionally.
A typical and more obvious situation is when first several places receive corresponding monetary prizes, and at the same time it costs money to enter into a tournament and/or continue engaging in the activity professionally. This immediately introduces a positive feedback loop, which begins to favor previous champions, increasing their chances of entering the next tournament and being able to engage in the activity full time. The unfairness of such a setup becomes clearer when monetary prizes for several top ranks differ from the rest by a magnitude.
For instance, in chess the significant difference in the amount of money awarded to the champion of the tournament and to the runner-ups makes it very challenging even for highly performant players to earn money by playing chess unless they are routinely winning tournaments. Thus, even some of the strongest players in the world might find it difficult to put as much time and effort into perfecting their game, since they might need to compensate their income by engaging in other work, while the several champions who receive large prizes are able to do chess professionally all the time and become even better at the game.
An even more overt mechanism is player seeding in tennis. In this case, the high ranking players routinely receive preferential treatment, especially at larger events: it is ensured that they will not be matched with anyone who is above a certain rank before the quarterfinals. This effectively decreases the probability that these top players are going to be eliminated early (by being spared the prospect of eliminating each other), and conversely decreases the probability of new players reaching the quarterfinals. At the same time, these large events can significantly add to the player's ranking. Thus, this positive feedback loop increases the chances that high ranking players earn the most points throughout the year and remain on top, while at the same time earning more money than the rest. Add to that the indirect effects of the costs of continuing to do tennis professionally, and the hidden benefits of being a famous player.
Therefore, by differentiating competition rules and ranking rules we can see how the knockout ranking is unfair by itself, but also how even more unfairness is introduced through direct and indirect positive feedback loops, which would tend to create an elite group of players who would tend to stick to the top of the ladder. Even in our case of identical skill levels, a system like player seeding is highly likely to create a group of players that would tend to stay in the top 8 across many competitions.
A lot of the literature on the subject is focused on analyzing empirical data of specific competitions. This framework demonstrates that in many, if not all, cases the level of fairness can be judged by simply analyzing how the competition is set up to begin with: a lot of very common ranking rules are inherently unfair or can only be fair if infinite time and resources are assumed.
By carefully outlining the relevant elements of a competition, the suggested framework is capable of modeling any such competition and reveal, quickly and convincingly, the conditions that give rise to both fairness and unfairness.
I believe that utilizing this framework can move the conversation regarding the role of luck in success quite significantly, by generalizing what a lot of papers on the subject are saying about specific data points.
Additionally, it focuses on the frequently ignored aspect of a competition: its ranking rules. By simply analyzing classes of common ranking rules used in our society, we are able to not just register the role of luck, but also convincingly explain how it arises in skill-based competitions.
This explains why I haven't run any simulations for the paper: the power of the framework is not in its ability to register the role of luck in a given set of empirical data, but in its ability to convincingly explain the mechanisms that give rise to luck in skill-based competitions.
And these mechanisms can be summarized as follows:
- If a competition is held between players of different skill levels, and if the difference between skill levels is larger than the amount of luck in a given competition, then the only thing that matters would be skill. In other words, no matter how lucky the less skilled player would be and no matter how unlucky the more skilled player would be, the more skilled player would still win. Comparisons of people with vastly different skill levels enforce the idea of meritocracy.
- The closer the skill levels of the players, the higher the role of luck. When a competition is held between players of identical skill, the role of luck becomes absolute. Most meaningful competitions in life occur between players with very similar skill levels, which could explain the pervasive role of luck in at least some empirical data.
- Ranking rules dramatically contribute to the fairness of the outcome and sometimes make the character of the activity irrelevant. In other words, regardless of how much a given activity relies on skill, if the ranking rules are unfair, the outcome of such a competition is going to be unfair as well.
- Many of these ranking rules have in-built positive feedback loops that tend to skew prizes towards previous winners.
- Finally, these insights are true for any competition.
Thus, my hope is that this framework can provide a unified way to talk about fairness, meritocracy and the role of luck in success.